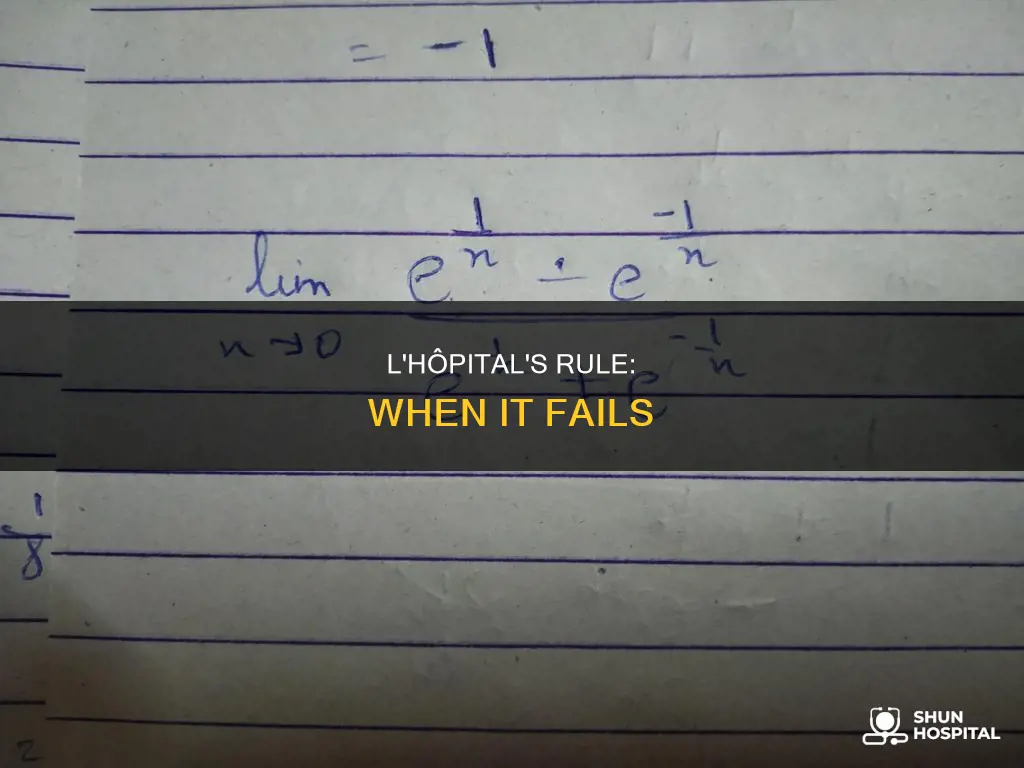
L'hôpital's Rule: When It Fails

L'Hôpital's rule, named after the 17th-century French mathematician Guillaume de l'Hôpital, is a method for evaluating indeterminate forms. However, it does not apply to all cases. L'Hôpital's rule specifically applies to indeterminate forms such as 0/0 or ∞/∞. It involves differentiating the numerator and denominator separately and then reevaluating the limit. However, if the limit does not yield an indeterminate form, applying L'Hôpital's rule can lead to incorrect results. Therefore, it is important to first determine if the limit results in an indeterminate form before applying the rule. Additionally, there are cases where L'Hôpital's rule may not simplify the expression, and alternative methods may be required.

When the limit does not give an indeterminate form

L'Hôpital's rule is a general method of evaluating indeterminate forms such as 0/0 or ∞/∞. It is used to evaluate limits that give indeterminate values by the application of a limit. The rule states that the limit of the ratio of two functions (where the denominator is NOT equal to 0) that results in an indeterminate form by the direct application of the limit is equal to the limit of the ratio of their derivatives.

L'Hôpital's rule can be applied more than once. You can apply this rule until it holds any indefinite form every time after its applications. However, if the problem is not in the indeterminate form, you cannot apply L'Hôpital's Rule. Application of L'Hôpital's rule when the limit does not give an indeterminate form throws the wrong result. For example:

Lim x → 2 (3x + 1) / (2x + 2) = (3(2) + 1) / (2(2) + 2) = 7/6 (correct answer)

The limit didn't result in an indeterminate form and so we can't apply L'Hôpital's rule. We know that the derivatives of 3x + 1 and 2x + 2 are 3 and 2, respectively. So, the above limit after the application of the rule becomes:

So, do apply the limit first and make sure that an indeterminate form is resulted before applying the rule.

Other indeterminate forms, such as 1∞, 00, ∞0, 0·∞, and ∞−∞, can sometimes be evaluated using L'Hôpital's rule. Indeterminate forms besides 0/0 and ∞/∞ include 0×∞, ∞−∞, 1∞, 00, and ∞0. These forms also arise in the computation of limits and can often be algebraically transformed into the form 0/0 or ∞/∞, so that L'Hôpital's rule can be applied.

When the functions are not continuous

L'Hôpital's rule is a general method of evaluating indeterminate forms such as 0/0 or ∞/∞. It is used to evaluate the limits of indeterminate forms for derivatives in calculus. The rule states that for functions f and g, which are defined on an open interval I and differentiable on an interval containing c, the limit of the quotient of the functions is equivalent to the limit of the quotient of their derivatives.

However, L'Hôpital's rule cannot be applied when the functions are not continuous. This is because one of the necessary conditions for the rule to be valid is that the functions f and g are continuous on the interval [a, b] and differentiable on the interval (a, b). If either function is discontinuous, the rule cannot be applied, and its conclusion may be false.

For example, consider the functions f(x) = x^2 and g(x) = |x| defined on the interval [-1, 1]. The functions are not continuous at x = 0, and applying L'Hôpital's rule would give an incorrect result.

In general, when dealing with discontinuous functions, other methods or techniques, such as the squeeze theorem, may be more appropriate for evaluating limits. It is important to carefully examine the functions and their properties before applying any specific rule or theorem.

Additionally, it is worth noting that L'Hôpital's rule should only be applied when direct substitution of the limit yields an indeterminate form. If the limit does not result in an indeterminate form, applying the rule will lead to an incorrect answer. Hence, it is crucial to first determine if the limit is indeterminate before considering the application of L'Hôpital's rule.

When the functions are not differentiable on an interval containing c

L'Hôpital's rule is a general method of evaluating indeterminate forms such as 0/0 or ∞/∞. It states that for functions f and g which are defined on an open interval I and differentiable on an interval containing c, the limit of the quotient of the functions is equivalent to the limit of the quotient of their derivatives.

However, it is important to note that L'Hôpital's rule is not valid if one of the four conditions is not satisfied. One of these conditions is that both f and g must be differentiable everywhere on an interval containing c. If the functions are not differentiable on an interval containing c, then L'Hôpital's rule cannot be applied, and attempting to do so may yield incorrect results.

For example, consider the limit as x tends to 2 of the quotient of (3x + 1) and (2x + 2). The limit of this expression is 7/6, which is not an indeterminate form. If we incorrectly apply L'Hôpital's rule, we find the derivatives of the numerator and denominator and evaluate the limit of their quotient, which gives 3/2, an incorrect result.

Another example is when the functions are not differentiable at the point of interest c. In this case, L'Hôpital's rule cannot be applied directly, and a workaround is required. One approach is to evaluate the limit as a difference of two functions and then convert it to a quotient. This allows us to apply L'Hôpital's rule and find the correct solution.

In summary, L'Hôpital's rule is a valuable tool for evaluating indeterminate forms, but it is essential to ensure that all conditions are met before applying it. When functions are not differentiable on an interval containing c, alternative methods or workarounds may be necessary to find the correct limit.

When the functions are not differentiable on the interval (a, b)

L'Hôpital's rule is a method used to evaluate the limits of indeterminate forms. It is named after the 17th-century French mathematician Guillaume de l'Hôpital, although it was first introduced to him by the Swiss mathematician Johann Bernoulli in 1694.

L'Hôpital's rule can be applied when functions are not differentiable on the interval (a, b). However, it is important to note that the rule requires both functions, f and g, to be continuous on the interval [a, b] and differentiable on the interval (a, b). This is a necessary condition for the rule to be valid. If any of the conditions are not satisfied, L'Hôpital's rule may yield incorrect results.

In such cases where the functions are not differentiable on the interval (a, b), it is still possible to apply L'Hôpital's rule by considering the limit of the quotient of the functions' derivatives. Specifically, the rule states that the limit of the ratio of two functions (where the denominator is not equal to 0) that results in an indeterminate form by direct application of the limit is equal to the limit of the ratio of their derivatives.

For example, let's consider the limit as x approaches 0 of (sin x) / x. This limit results in an indeterminate form of 0/0. By applying L'Hôpital's rule, we can find the limit by taking the derivative of the numerator and denominator separately and then evaluating the new limit.

It is important to note that L'Hôpital's rule should only be applied when direct substitution results in an indeterminate form. If the limit does not give an indeterminate form, applying the rule can lead to incorrect results.

When the problem is not out of the indeterminate forms

L'Hôpital's rule is a general method of evaluating indeterminate forms such as 0/0, ∞/∞, 0×∞, ∞−∞, 1∞, ∞0, and more. It is used to evaluate the limits of indeterminate forms by finding the derivatives of the numerator and denominator and applying the limit. This rule can be applied repeatedly until a defined value is obtained.

However, L'Hôpital's rule is not always applicable. It is important to note that this rule is specifically designed to handle indeterminate forms. If the problem is not in an indeterminate form, L'Hôpital's Rule cannot be applied. For example, consider the expression lim x → 2 (3x + 1) / (2x + 2). The limit of this expression does not result in an indeterminate form, and applying L'Hôpital's rule would give an incorrect result.

In some cases, applying L'Hôpital's rule may lead to cyclic expressions where repeated applications bring us back to the original expression. In such situations, intermediate simplifications or substitutions might be necessary to break the cycle and solve the problem.

Additionally, L'Hôpital's rule assumes certain conditions for its validity. For instance, it requires that the functions involved be continuous and differentiable on the interval of interest. If these conditions are not met, the rule may yield incorrect conclusions.

Furthermore, while L'Hôpital's rule simplifies finding limits of indeterminate forms, it is not the only method available. Other techniques, such as the squeeze theorem, can also be used to evaluate indeterminate forms without relying on L'Hôpital's rule.

In summary, L'Hôpital's rule is a valuable tool for evaluating indeterminate forms, but it is not universally applicable. It is essential to recognize when the problem is not in an indeterminate form and explore alternative methods or simplifications to arrive at the correct solution.

Frequently asked questions